
최대공약수랑 최소공배수 사이의 관계를 찾아보다가 알아낸게
두 수의 곱이 최대공약수 * 최소공배수 라는 것이었다.
나름 이과에 공대출신인데 기억이; 하나도 안났죠..?
두 수의 최대공약수는 유클리드 호제법을 사용해야 한다고 하고.. 구한 최대공약수를 이용해 최소공배수를 구해야 한다!
유클리드 호제법이란?
유클리드 호제법은 두 개의 정수(자연수) 사이에서의 최대공약수를 구하는 알고리즘이다.
호제법이란 말은 두 수가 서로 상대방 수를 나누어서 결국 원하는 수를 얻는 알고리즘을 나타낸다.
2개의 자연수(또는 정식) a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다. 이 성질에 따라, b를 r로 나눈 나머지 r'를 구하고, 다시 r을 r'로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수이다.
-위키백과
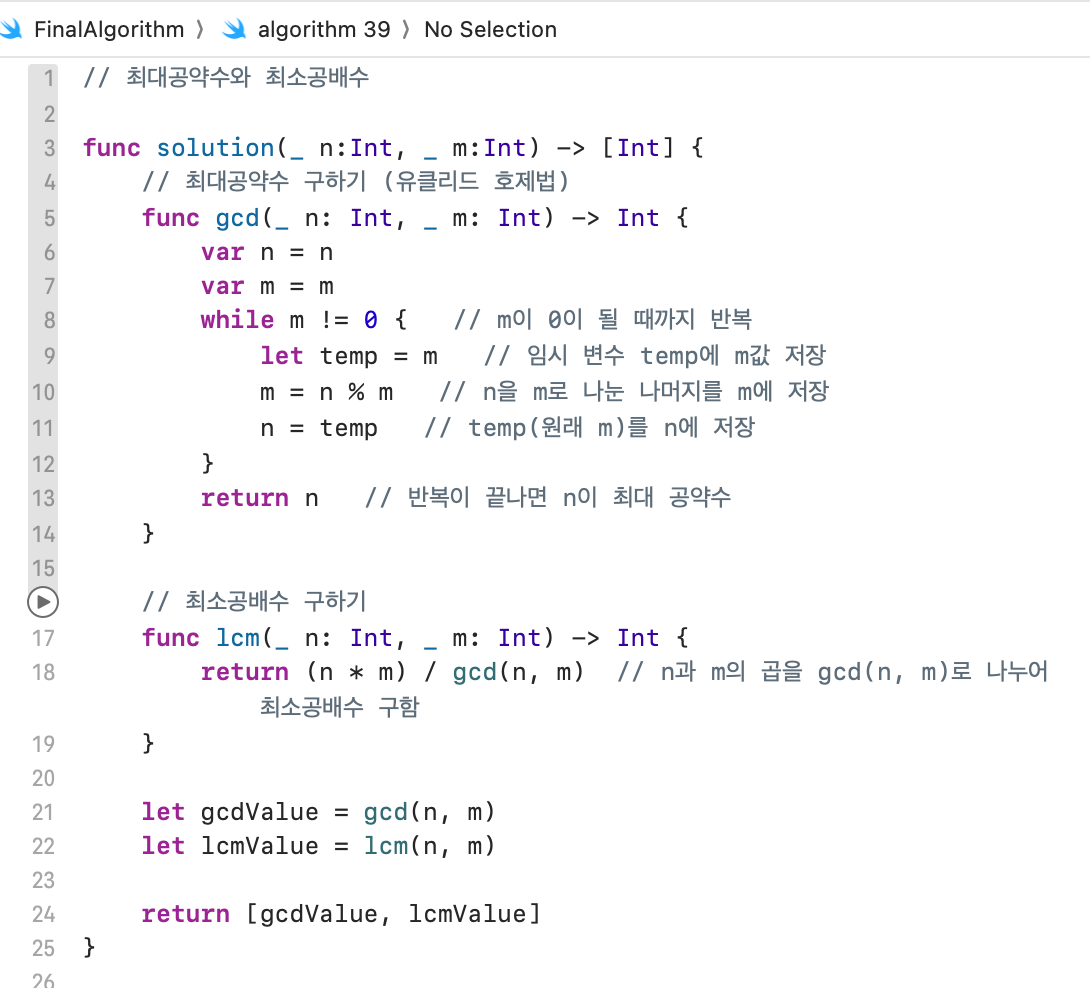
gcd는 최대공약수를 의미하고 lcm은 최소공배수를 의미한다.
temp는 임시 변수로 유클리드 호제법을 사용하여 최대공약수를 구할 때 값의 교환을 위해 사용한다.
임시 변수를 사용하지 않고 값의 교환을 바로 하면 문제가 발생할 수 있는데,
만약 바로 n에 m을 대입하고 m에 n % m 을 대입하면, m의 값이 바뀌기 때문에 원래 m의 값을 잃게 된다.
따라서 임시 변수 temp를 사용하여 m의 원래 값을 보존한 후에 교환을 진행한다.
임시 변수를 사용하지 않고 교환하는 방법도 있다.
스위프트의 swap 함수를 사용할 수 있다.
func gcd(_ a: Int, _ b: Int) -> Int {
var n = n
var m = m
while m != 0 {
(n, m) = (m, n % m)
}
return n
}이 방법을 사용하면 임시 변수를 사용하지 않고 두 값을 교환할 수 있다.
'알고리즘 문제풀이' 카테고리의 다른 글
| 41. 이상한 문자 만들기 (0) | 2024.06.26 |
|---|---|
| 40. 3진법 뒤집기 (0) | 2024.06.25 |
| 38. 직사각형 별찍기 (0) | 2024.06.21 |
| 37. 행렬의 덧셈 (0) | 2024.06.20 |
| 36. 문자열 다루기 기본 (0) | 2024.06.19 |



